Cálculo de Proposições

Pergunta. O que significa “oração” na linguagem comum? Lembra-se de alguma constatação sobre “um verbo”? Há possibilidade de ter uma oração com 47 verbos? E quais são os sinônimos de “oração”?

(Dicas. Apresente exemplos de vários tipos de frases: com sentido, sem sentido, que transmitem um claro recado possuindo apenas uma ou duas palavras, as vezes não tendo um verbo, expressões da linguagem particular... Só na base de dados concretos pode-se partir para umas generalizações.)

A decisão de simplificação leva à seguinte definição usada na matemática: criamos duas gavetas, uma para constatações verdadeiras, outra para constatações falsas. O que couber nelas chamaremos de proposições – deste modo ficará claro que não estamos falando sobre as “orações da língua portuguesa”. Portanto trabalhamos só com as construções que não deixam dúvidas sobre a existência de objetos descritos, sobre sentido, sobre coringas (“variáveis”) e não se preocupamos como estabelecer a qual das gavetas uma constatação pertence. O conjunto de todas essas constatações denotamos por , o fato que a constatação está verdadeira destacamos usando a notação , para falsa escrevemos e podemos imediatamente partir para a próxima pergunta:
Como descrever a construção de “negação” na linguagem formalizada da matemática?

O que nega-se? As proposições? Ótimo. E que tipo de objeto é uma proposição negada? É de novo uma proposição? Então como descrever a função “negação”? (Quer dizer: qual é o seu conjunto de partida? e de chegada?)

A negação é uma função definida no conjunto de proposições, seus valores são também proposições e a sua atuação consiste em modificação do valor “verdade” ou “falso” de cada proposição. Notação formalizada:

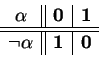
(A primeira linha descreve o nome do argumento e a listagem dos argumentos. A segunda – a notação do valor e a listagem dos valores correspondentes.)

O que pode ser feito ainda quando só uma variável percorre o conjunto de proposições? Há uma outra função evidente, a que “não faz nada” – que a cada atribui o valor . Na sua opinião, qual seria o nome adequado para ela? Conhece o nome que ela de fato ganha na matemática? Consegue descrevé-la por meio de uma tabela parecida com a anterior?

Pergunta. Há outras possíveis funções de 1 argumento lógico (isto é, que dependem de uma variável só)?

Reformulação: é possível inventar outras tabelas de funções que levam o conjunto em ?
Quantas? Como descobrir a quantidade sem de fato construí-las? Qual sentido elas teriam (quer dizer: há algum tipo de construção em língua portugesa a qual tal função corresponderia?)

Passamos agora a analizar as construções que envolvem duas proposições. Naturalmente a primeira delas é aquela que junta umas proposições usando a palavra “ou”. Isto é: a altenativa.

Procure encontrar (por sua própria conta, sem a ajuda dos livros ou professores da Universidade) várias diferênças entre o cotidiano sentido de “alternativa” e este termo em suas aplicações matemáticas (que inevitavelmente você já viu com frequência). Só depois passe a analizar a questão:

Como na lógica matemática define-se a “alternativa”?

Alternativa é uma função que atribui a cada par de proposições uma nova proposição do modo que o valor lógico de proposição obtida pode dar “falso” somente se ambos os argumentos são falsos. Em uma notação formalizada:

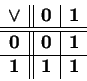
(Esta vez não faço uma listagem de todas as possíveis quatro configurações de argumentos e correspondentes valores que atribuo a eles. Uso uma notação mais sucinta, conhecida desde a 3ª serie de 1º grau – a de tabuada. Os pares de argumentos estão colocados em linhas e em colunas. Os obtidos valores encontram-se no cruzamento de adequada linha com adequada coluna.)

Considere agora as seguintes funções:

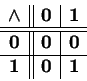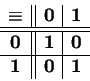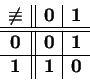Na vida real a mais importante de todas elas parece ser a implicação. Aqui vem a sua definição.

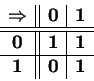
Logo vamos ver como são importantes as seguintes relações entre os nossos novos objetos – importantes pois descrevem de modo excelente as ligações entre aquelas construções da língua natural que deram origem a nossas formalizações matematizadas.

Leis de De Morgan (como negar uma alternativa ou uma conjunção):

Como dizer “se ... então ...” não usando a palavra “se”, expressando a proposição em forma “ou ... ou ...”?

Como negar a implicação?

A lei de contraposição:

Uma contradição:

Uma tautologia (a lei do meio excluido):

O essencial é compreender bem como divergem os sentidos da mesma palavra se ela aparece na nossa vida em dois sentidos: o costumário, adquirido no uso cotidiano da língua portuguesa e o novo sentido técnico, de formalização trazida de aula ou de um livro-texto.

Espero que você lembra bem como divergem os sentidos de “oração” em português e “proposição” em “matematiquês”. Parece que não há graves divergências entre os sentidos da “negação”. Mas não é o caso da alternativa.

Parece que na linguagem comum entende-se que

• alternativa é cada uma das duas opções que são conectadas pela palavra “ou” (quer dizer: em expressão “isso oui outro” temos duas alternativas);
• as opções têm alguma conexão pelo sentido;
• com freqüência as opções são excludentes (não se cogita que ambas as opções sejam realizadas simultaneamente);

A formalização matemática trata a alternativa com um par das opções e nenhuma das demais exigências é imposta sobre as proposições que aparecem na alternativa.

Quero destacar um fato, bastante indesejável. Observa-se com certa frequência que os profissionais apegam-se tanto ao sentido técnico de algum termo da sua gíria que passam de tratar com ironia os seus usos cotidianos. Vejo as vezes essa atitude no caso de alternativa – cada vez que alguém anuncia na TV “temos aqui duas alternativas” um matemático comenta maliciosamente: “ah, então são quatro possibilidades!” Admito que também eu tenho tentação de corrigir o estranho emprego daquele termo que uso em outra maneira no meu cotidiano matemático mas um momento de reflexão calma força-me a reconhecer que não é um lugar adequado para bairrismos linguísticos. Uso diferente não significa uso pior. É apenas diferente – e completamente legítimo. E não compensa iniciar guerras santas em nome de diferenças em definições aceitas no seu ambiente.

E quais são as diferenças entre os dois sentidos – costumário e formalizado – no caso de conjunção? Na linguagem comum aqui também espera-se que há alguma ligação entre os os sentidos das proposições (a conjunção “vou cruzar a rua e Camões escreveu em português” não seria aceita pacificamente por maioria de pessoas). Mas além disso surge um outro elemento complicador: juntando duas proposições em uma por meio da palavra “e” criamos uma narrativa que está assentada no tempo e compreendemos (sem mencionar esse fato) que a primeira parte da conjunção acontece antes da segunda; portanto a conjunção “cotidiana” não é bem comutativa; o meu exemplo preferido é a diferença no tamanho do prato no caso das expressões “nos almoçamos e João veio” e “João veio e nos almoçamos”.

De novo: a versão da palavra aceita matematicamente é imune a essas nuanças: a tabela que define a conjunção tem uma visível simetria com respeito a diagonal – portanto a comutatividade é garantida pela construção da função (a troca da sequência de argumentos não afeta o valor da função) e não se menciona exigência qualquer sobre o conteúdo das proposições que estão sendo juntadas.

Mas a construção que traz as maiores dificuldades conceituais é a função implicação. As dificuldades de negar, reformular ou disprovar uma implicação são bem conhecidas e muito significativas. Indicam elas que a palavra “então”, apesar de parecer inocente, tem muito conteúdo bastante complexo. (Quem sabe se não é uma das mais importantes palavras na ciência?) O seu trabalho vai ser mais simples se você guardar na memória o fato seguinte:

Isto é: os raciocínios hipotéticos, aqueles “experimentos virtuais” da ciência, não giram ao redor da validade ou falsidade da tese. No trabalho com uma expressão da forma não se procura comprovar mas conferir se existe um caminho que liga com . Do mesmo jeito como no caso de alternativa, não importa para nós o “sentido” ou “significado”das proposições.